
The Nobel laureate Richard Feynman famously stated that, “nobody really understands quantum mechanics”. This statement is often used to underline the fundamental limit of our physical understanding. For some, however, the only limit delineated by this famous statement is that of one’s own imagination.
Quantum mechanics is a theory that was crafted over many decades to explain robust experimental observations, thus it is not overly surprising that it works so well. What is surprising, at least to me, is that even to this day scientists cannot agree on a sensible physical picture, which could be attached to this incredibly successful theory. This lack of a physical picture is what, at first, led me, as well as many others, away from quantum mechanics. Interestingly, it was also what brought me back.
My turnaround started when I encountered a new and beautiful area of research called Hydrodynamic Quantum Analogs, where droplets bouncing on a fluid surface are used to better understand quantum mechanical systems. Since my research interests always revolved around interfacial phenomena (which is all the magical stuff happening on interfaces between different fluids), I found these quantum droplets irresistible. Luckily, I was awarded a Fulbright fellowship, which allowed me to do my postdoctoral research at MIT, with one of the world’s leading groups in the field. The goal of this article is to give a quick exposition, an aperitif of sorts, to this fascinating field.
The Merriam-Webster dictionary defines an analog as: “something that is similar or comparable to something else either in general or in some specific detail”. In science, we often study analogous systems when one of the systems is much more accessible to experimental probing than the other, typically because of the very different scales associated with each system. Often it is possible to obtain valuable insight into the nature of an inaccessible phenomenon by observing a much more accessible analogous system.
Fluid dynamics provides an especially fertile framework for finding surprising analogs of various non-fluidic systems. For example, super-fluids can be accelerated beyond the speed of sound, creating an acoustic event horizon, which is analogous to the event horizon of black holes, and even produces Hawking radiation [1]. A simple hydraulic jump that occurs in one’s sink around the central stream of water pouring from the faucet, is a surprisingly good analog for a theoretical object from the theory of general relativity, known as a white hole [2]. These fluid-dynamical systems provide us with a window to phenomena occurring at the very large scale - so large in fact, that it is not accessible to probing with our current technology.
But what about the very small scale? Newton described corpuscles of light generating waves through the ether like stones dropped on a pond, while Thomas Young argued the wave nature of light by analogy with ripple tank experiments. Surprisingly, these two very different pictures, which underline the illusive nature of the particle-wave duality, can in fact be reconciled through one beautiful analog.
Our story begins with a peculiar phenomenon that occurs when a millimeter-sized droplet is placed on a vibrating bath containing the same liquid. One’s intuition says that the droplet should coalesce with the bulk liquid almost immediately; however, as we will see, the droplet can keep bouncing on the liquid surface indefinitely, without coalescing.
This non-coalescence phenomenon is possible due to a thin layer of air trapped between the droplet and the liquid surface. As the droplets moves closer to the liquid surface and the intermediate air layer becomes thinner, it begins to behave as a viscous fluid and opposes drainage. If the droplet were placed on a quiescent liquid, the thin layer would eventually drain, and coalescence would occur. If, however, the liquid surface is forced to vibrate in a specific range of frequencies and amplitudes, the droplet will be pushed back up, away from the liquid, preventing coalescence.
Each time the droplet bounces off the liquid surface, it creates a surface wave that travels radially outwards from the point of impact. These bouncing droplets can communicate between them through their emitted wave fields and have even been shown to self-organize into crystalline structures [3] through this interaction (Fig.1a). It is important to note that if the force increases beyond a certain limit, which is called the Faraday threshold, the initially flat liquid surface will destabilize into a pattern of standing waves, which will disturb any occurring structures.
In 2005, Yves Couder and Emmanuel Fort discovered that close to this Faraday threshold the droplet can come into resonance with its emitted wave field, at which point it will spontaneously self-propel along the liquid surface, guided by the wave field it itself generates [4] (Fig.1b). Close to the Faraday threshold, the waves emitted by the droplet excite the lowest Faraday mode, which is sustained by the vibrations and does not decay for a very long time. The proximity of the forcing to the Faraday threshold can therefore be described by a “memory” parameter – the closer one is to the threshold, the larger the memory. At high memory, the waves emitted in the previous bounces are sustained by the vibrations, and the droplet interacts not only with the wave emitted in its previous bounce, but with a superposition of many waves emitted throughout the droplets’ history. In this sense, the droplet “remembers” its past.

Fig. 1. (a) Bouncing droplets in a crystalline structure. (b) A walking droplet in a high memory regime. Photo credit: Daniel M. Harris.
It turns out that droplets guided by their own resonant wave field bear a remarkable resemblance to the pilot-wave picture of quantum mechanics originally proposed by Louis de Broglie in 1927 [5]. In that picture, a quantum particle (e.g., an electron) is a localized object oscillating at a frequency proportional to its Compton frequency, and moving in accordance with its spatially extended pilot wave.
Shortly after their discovery, walking droplets were demonstrated to behave in ways reminiscent of quantum mechanical particles. The first wave of these quantum-like effects included single particle diffraction, quantum tunneling, quantized orbits, orbital level splitting, spin states, and many others [6]. Many of these effects had no classical analogs before they were observed in the bouncing droplets system.
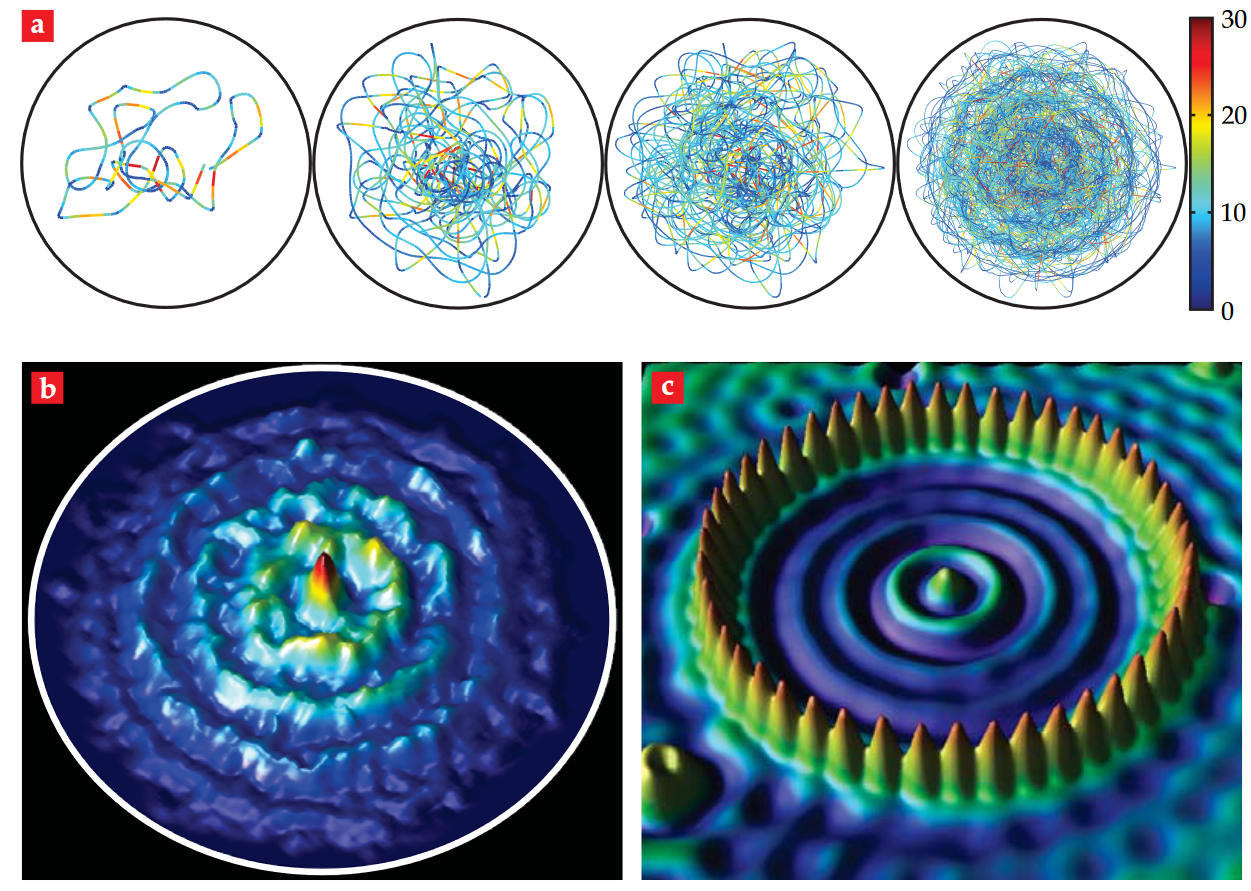
Fig. 2. A walker in a circular corral. The high-memory trajectories of increasing length depicted in (a) are color coded according to droplet speed in millimeters per second. (b) The histogram of the walker’s position corresponds roughly to the amplitude of the corral’s most unstable Faraday mode. The emerging statistics of the confined walker are reminiscent of (c) the statistics of electrons in a quantum corral. Figure adapted with permission from Harris et al. (2013). Copyright 2013, AIP Publishing LLC.
The next significant breakthrough happened when Couder’s group joined forces with John Bush’s group at MIT, to study the long-term statistics of a walking droplet confined to a circular corral. It turned out that coherent wavelike statistical behavior emerges from the complex underlying dynamics of the walking droplet. In fact, it was shown that the probability distribution for the position of the droplet is prescribed by a specific wave mode of the corral, surprisingly similar to the probability distribution of an electron in a quantum corral7.
This result led to a second wave of discoveries, where important phenomena such as Friedel oscillations and the Kondo effect were demonstrated through hydrodynamic analogs.
This hydrodynamic system is, of course, not without its limitations. For starters, since the droplets can only move in a plane, three-dimensional effects are currently very difficult to obtain. In addition, quantum-like behavior arises only at high memory; however, due to viscous effects, the memory in a real hydrodynamic system cannot be pushed to infinity. It is also very likely that real quantum mechanical systems are not entirely hydrodynamic in nature, and some key features of quantum theory simply cannot be captured through hydrodynamic analogs.
With that said, hydrodynamic quantum analogs introduce a new perspective and new ways of visualizing quantum phenomena. Hopefully, in time, these new ideas will inspire novel approaches to the foundations of quantum mechanics, helping us to better understand this important theory of nature.
References:
1. Steinhauer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nature Physics 12, 959–965 (2016).
2. Schützhold, R. & Unruh, W. G. Gravity wave analogues of black holes. Phys. Rev. D 66, 044019 (2002).
3. Eddi, A., Decelle, A., Fort, E. & Couder, Y. Archimedean lattices in the bound states of wave interacting particles. EPL 87, 56002 (2009).
4. Couder, Y., Protière, S., Fort, E. & Boudaoud, A. Walking and orbiting droplets. Nature 437, 208–208 (2005).
5. de Broglie, L. Interpretation of quantum mechanicsby the double solution theory. Ann. Fond. 12, (1987).
6. Bush, J. W. M. Pilot-Wave Hydrodynamics. Annu. Rev. Fluid Mech. 47, 269–292 (2015).
7. Harris, D. M., Moukhtar, J., Fort, E., Couder, Y. & Bush, J. W. M. Wavelike statistics from pilot-wave dynamics in a circular corral. Phys. Rev. E 88, 011001 (2013).

Articles are written by Fulbright grantees and do not reflect the opinions of the Fulbright Commission, the grantees’ host institutions, or the U.S. Department of State.


